Critical Chain Method

Published: 2013-03-27
Last updated: 2022-03-20

In his book Critical Chain, Eliyahu M. Goldratt introduced the critical chain method for planning and controlling a project. In its essence, it is the application of the theory of constraints (ToC) to project management, as we mention it in sub-section Triple Constraint.

Let us explore what problems the critical chain method addresses, how it works and what it changes in our project planning and controlling approach.

Typical Problems in Project Planning and Implementation

For many projects that suffer delays we observe these typical problems or phenomena:

(A)    By carefully estimating each project task’s duration and effort most experts include extra or hidden buffer into each task to “be on the safe side”. This minimizes the overall project buffer.

(B)    “Student Syndrome”: Team members tend to wait too long until they start their work on project tasks and thus, consume most of the tasks’ hidden buffers.

(C)    Due to scarce human resources team members have to work in multi-tasking mode, and this multi-tasking within one project delays the start of work on any given task.

(D)    Although duration and effort of tasks are carefully estimated and contain hidden buffers, delays accumulate while advances remain unutilized.

Analysis of an Example

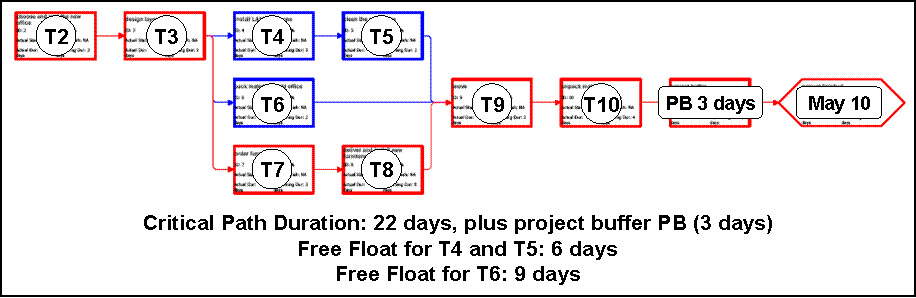
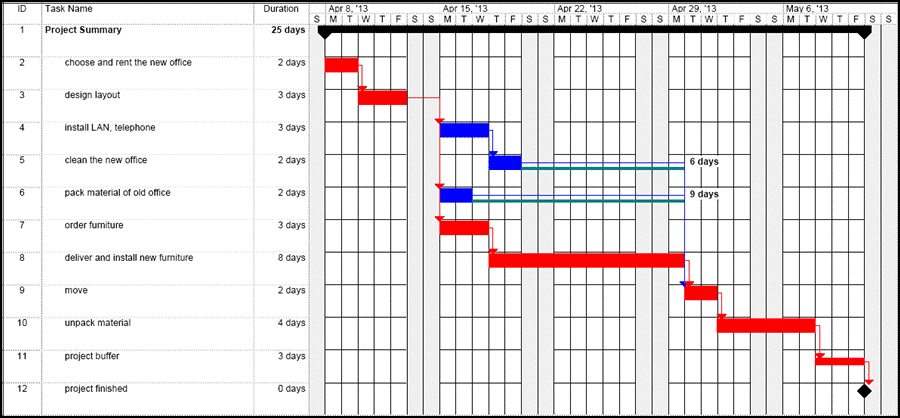
Using the example of the move of an office we could find the following situation in planning phase. As usual, we set up a project plan with the WBS of project tasks including estimated durations, the Gantt chart and the network diagram

CPM Network Diagram

CPM Gantt Chart

So far, we use the same approach as in the sub-section Planning the Project Schedule, and we obtain as planning result: If the project has to be complete by May 10, the total float or project buffer is 3 days, tasks T4 and T5 have free float of 6 days, and task T6 has free float of 9 days.

In case we do not address the problems described in (A), (B), (C) and (D) we most likely will face a critical situation towards the end of that project: it is morning of May 10, all buffers are gone, task T10 (unpack material) just started and hope is gone to complete the task before the weekend.

Changing the Way of Thinking: Critical Chain Method

How does the method of critical chain as a result of the theory of constraints address those problems?

Applying the theory of constraints, we interpret problems (A) hidden buffers, and (B) the student syndrome, as symptoms of a deeper lying problem with the policies of the organization: we might have a culture in which the organization punishes delayed task completion, and / or, at the same time, does not reward early completion.

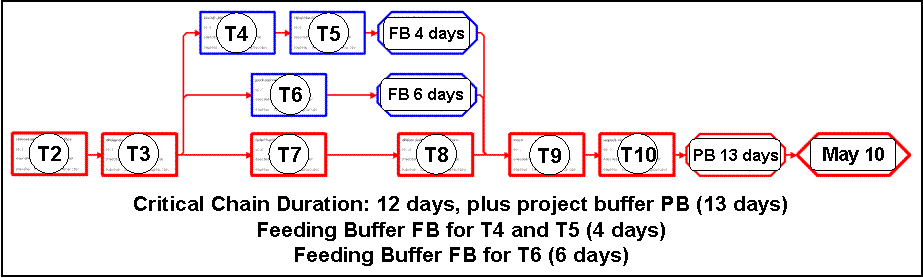
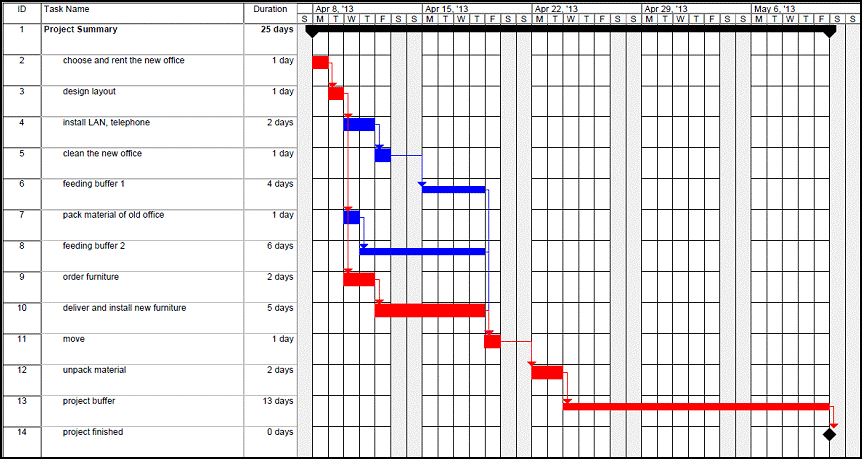
If we successfully change this culture by rewarding early completion without punishing delays we might be able to remove both: hidden buffers in effort estimation and the student syndrome. In our example, the experts could give us the best case estimation of the duration of each task by disclosing the hidden buffer. Then, estimated durations, Gantt chart and network diagram would look like this

*) if the milestone date remains the same

Critical Chain Method: Network Diagram

Critical Chain Method: Gantt Chart

In this network diagram, we re-arrange the tasks on the critical path into the critical chain, while the tasks T4, T5 and T6 remain on two non-critical paths, both “feeding” work results into the critical chain. We collect all the hidden buffers into two feeding buffers (for T6, FB = 6 days before T9; for T4 and T5, FB = 4 days, before T9) and the project buffer PB = 13 days (if the end milestone remains unchanged.

This describes the core of the critical chain method in project planning.

In project implementation, the critical chain method focuses on rewarding early completed tasks and ensuring unbiased and facts-oriented problem solving – no finger pointing, no blaming, no punishment – in case of unexpected events in order to keep the project buffer clear of consumption and to avoid the unproductive search for excuses or alibis.

Comments:

1. The critical chain method applied to problem (C), would lead to similar results if we first setup the critical chain based on those scarce human resources, and then, follow the same course as described above.
2. Problem (D) seems to call for similar organizational cultural changes as in our example above: reward early finish, no punishment for delays.
3. The proposed organizational changes in the culture of rewarding early completion of tasks may still become subject to worry: Imagine, one of the experts in your project over-estimates the duration of his tasks in the first place, just to enable him to finish early and earn his reward. Project, line and general managers around the whole world and across all industries are desperately looking for some realistic ways out of this dilemma. If you have any ideas please let us know.
4. Avoiding punishment, finger pointing and blaming, is a major cultural change worthwhile to try anyway. This already might improve the project delivery times significantly, even without explicit application of the critical chain method.
5. Our example above shows, that we need a diligent analysis of the critical path of a project which we want to further plan and control using the critical chain method. For that critical path analysis, in turn, we need careful effort and duration estimation as well as scheduling of all project tasks / work packages.
   

For further details, please refer to Eliyahu M. Goldratt, Critical Chain, 1997